
The last trick is worth 10 points under all methods.Īces and Tens are worth 10 points, kings and queens are worth 5 points, jacks and nines are worth zero.Īces are worth 11, tens are worth 10, kings are worth 4, queens are worth 3, jacks are worth 2, and nines are worth zero. There are several ways to count up the points for play, but they add up to 250 points under all methods. Points are scored based on the play of the hand. So, if player A leads clubs, and player B and C have no clubs, both player B and C must ruff, and player C must overruff player B if possible. Further, when a previous player has ruffed and you also must ruff, you must overruff if possible. If you have neither of these cards, you may play any trump you wish, and if out of trump you may play any card you wish. So, if the trump king is led, you must play the ten or ace if you are next to play. When trump is led or played, you must beat the previous card played. Otherwise, each player must trump if possible. Each player must follow suit if possible. The high bidder leads to the first trick. As a shortcut, this is called a "roundtable".Īs normal with trick-taking games, the winner of each trick leads to the next. As a shorthand, some people divide all scores by 10 points.Īlso note that a marriage in each suit is worth 240 total points. But, with SK SQ DJ, the spade queen may be used both for a marriage and for a pinochle. So, HK HK HQ only counts as one marriage. "Double Pinochle" - both Jack of Diamonds and both Queen of Spades - 300 points.Įach card may be used in at most one meld of each class. "Pinochle" - Jack of Diamonds and Queen of Spades - 40 points. "Flush" - ATKQJ of trump suit - 150 points "Marriage" - King and Queen of nontrump suit - 20 points "Trump Marriage" - King and Queen of trump suit - 40 points The SA, HA, HA, and CA does not qualify for aces because you are missing the DA. It is important that they are different suits. "Jacks" - 4 jacks of different suits - 40 points "Queens" - 4 queens of different suits - 60 points
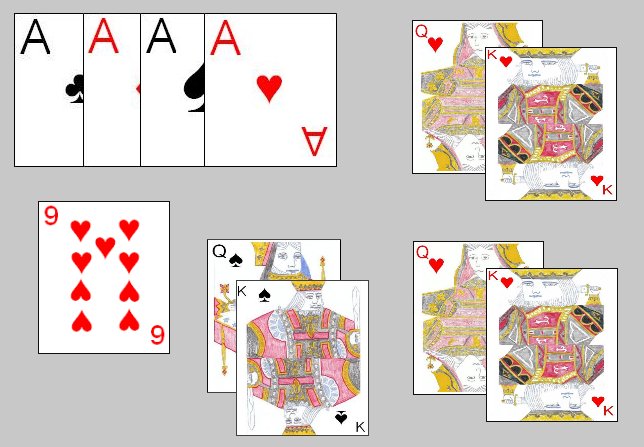
"Kings" - 4 kings of different suits - 80 points "Aces" - 4 aces of different suits - 100 points

Possession of these combinations adds points to one's score, and also confers partial information about one's hand to one's teammate and opponents. Meld consists of specific combinations of cards. If all players other than the dealer pass, the dealer names trump at a "price" usually one less than the minimum bid. A player who has not yet "passed" has the option of exceeding the current highest bid, or "passing". Bidding starts at a defined minimum level (150 for four handed pinochle). What is being bid on is the right to name a suit "trump", or higher ranking than all other suits in the taking of tricks. Each hand is played in three phases: bidding, melds and tricks. Hands are played until a player or team reaches 100 points. In general, dealing and play proceed from right to left. Variants of pinochle can be played by two, three, four, five or six players. Note that 10's rank higher than face cards. There are $24$ different cards, and there are $\binom$ for the probability.PinochlePinochle is a card game played with a 48-card pack consisting of two copies each of cards of the ranks 9, jack, queen, king, 10, ace in the four suits (spades, hearts, diamonds and clubs) found in the more widely used 52-card bridge or poker pack. For the count, we calculate the number of each type, and add up. Then there are $3$ types of $5$-card hands: (i) all cards distinct (ii) there is $1$ pair of identicals (ii) there are $2$ pairs of identicals. So for the count I will assume that for example the two $\heartsuit$ Queens are identical. So would the Pinochle probability be = 624/48C5 ?Ĭ) Probability of a royal flush (A,K,J,Q, 10 all of the same suit)Īttempt: P(Royal Flush) = 8/(48 C 5) = 1/214038

How would the numbers be changed? I know the technique is the same, but which numbers would end up changing?
#TWO HAND PINOCHLE HOW TO#
Calculate the following from the Pinochle deck:Ī) Total number of 5-card Poker hands possible (order does not matter)Īttempt: 48C5 = 1712304 (I believe this number includes repetitions, how do I get rid of those?)ī) Probability of a four of a kind (4 cards of the same denomination plus one card of a different denomination)įor this one, I know how to do it with a standard deck, as following, but not the Pinochle one. Poker can be played with the Pinochle deck, but the probabilities are different from poker with a standard deck. it consists of two copies of each of the 9, 10, J, Q, K and Ace of all four suits (so there are 2 nine of clubs, 2 nine of diamonds, 2 nine of hearts, two nine of spades, and so on for ever other denomination). A Pinochle deck is a special deck of cards with 48 cards in total.


 0 kommentar(er)
0 kommentar(er)
